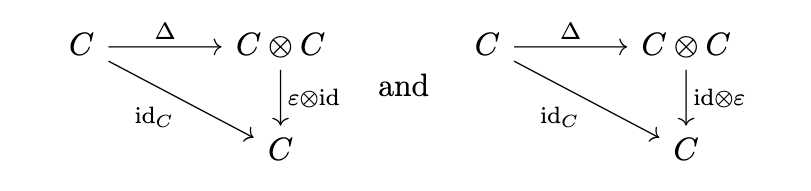Algebra and Coalgebra
Definition.
An -algebra is a monoidal object in -.
That is, an module , a linear map , called multiplication and the unit map .
It satisfies following diagrams
Associative Law:
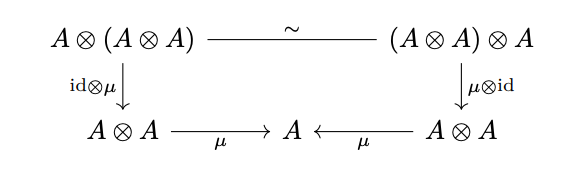
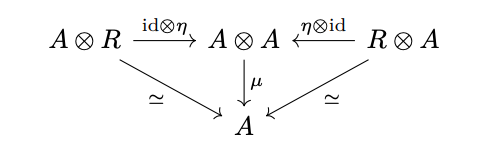
Unit Law:
Definition. A co--algebra is a comonoidal object in -.
That is, an -module , a comultiplication , and a counit map . Then reverse all the arrows in the above diagrams, i.e.
Coassociative
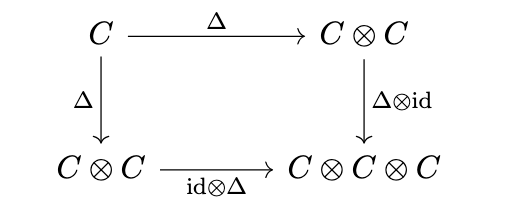
i.e.
Counit
The counit axioms are captured by two triangles:
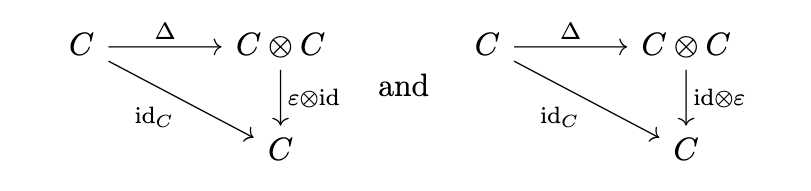
i.e.
Coalgebra and Leibniz rule for higher-order derivatives
Binomial Coalgebra
Consider the ring of polynomials . View it as a vector space over .
Define and by:
It is called binomial coalgebra.
Now let us check it forms a coalgebra. Since is a -alg homomorphism and is polynomial ring, we only need to check the value at for
and
Hence we have the identity
For
Consider
By symmetry we have . Hence it is a coalgebra.
Leibniz Law for higher-order derivatives
Now let us consider the Leibniz Law via this structure.
Consider and . Then .
The Leibniz law tells us that
Lemma. Let be a morphism and . If , then .
Proof.
We use mathematical induction here.
Assume that , then
Hence we have
Input we get
That is
In general, let be a differential ring and be the constant ring with respect to .
Then we could consider the coalgebra of . Again, ...We prove the Leibniz rule for higher-order derivatives for arbitrary differential ring.
The binomial coalgebra shows why the Leibniz Law looks like the binomial theorem.