Topic in Quiver

Math Essays: Quiver: (1) Basic definition and Pass algebra (marco-yuze-zheng.blogspot.com)

Quiver: (1) Basic definition and Path Algebra

Category of Directed Graph/Quiver

Definition. A quiver $Q$$Q$ is a directed graph $Q=(Q_0,Q_1,s,t)$$Q = (Q_0, Q_1, s, t)$, possibly with multiple arrows and loops. Here $Q_0$$Q_0$ is the set of vertices and $Q_1$$Q_1$ is the set of arrows. $s,t:Q_1\to Q_0$$s, t: Q_1 \to Q_0$ give you the source and target of arrows.

$$\begin{array}{}\text{(1)}& s(\alpha )\stackrel{\alpha }{\to }t(\alpha )\end{array}$$

We say an edge $e$$e$ is a loop if $s(e)=t(e)$$s(e) = t(e)$, and $Q$$Q$ is finite/countable if both $Q_0,Q_1$$Q_0, Q_1$ are finite/countable.

Example of Quiver

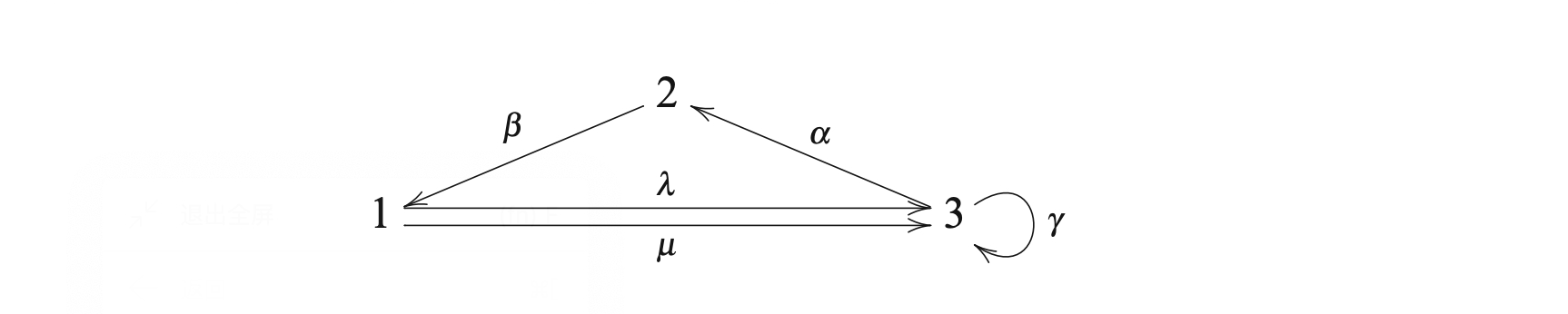
Let $Q_0=\mathbb{Z}$$Q_0 = \mathbb{Z}$, we define an edge $e$$e$ such that $t(e)=a$$t(e) = a$ and $s(e)=b$$s(e) = b$ if $a\le b$$a \le b$ and $gcd(a,b)=1$$\gcd(a, b) = 1$. Then we get a quiver.

Every small category is a quiver as well.

Definition. Category of quivers/directed graphs, $\mathrm{DGraph}$$\mathrm{DGraph}$

Let $Q=(Q_0,Q_1,s,t)$$Q = (Q_0, Q_1, s, t)$ and $Q^{\prime }=(Q_0^{\prime },Q_1^{\prime },s^{\prime },t^{\prime })$$Q' = (Q_0', Q_1', s', t')$ be two quivers. We define a morphism between $Q$$Q$ and $Q^{\prime }$$Q'$ to be a pair

$$\begin{array}{}\text{(2)}& (\alpha :Q_0\to Q_0^{\prime },\beta :Q_1\to Q_1^{\prime })\end{array}$$

such that $s^{\prime }(\beta (e))=\alpha (s(e))$$s'(\beta(e)) = \alpha(s(e))$ and $t^{\prime }(\beta (e))=\alpha (t(e))$$t'(\beta(e)) = \alpha(t(e))$. That is, it preserves edges.

Example

Let $\mathcal{C}\mathcal{,}\mathcal{D}$$\mathcal{C, D}$ be two small categories, and let $F:\mathcal{C}\to \mathcal{D}$$F: \mathcal{C} \to \mathcal{D}$ be a functor. Notice that a functor preserves commutative diagrams, hence it is a morphism between two graphs. Let $f:X\to Y$$f: X \to Y$ be a morphism in $\mathcal{C}$$\mathcal{C}$, then $s^{\prime }(F(f))=F(X)=\alpha (s(f))$$s'(F(f)) = F(X) = \alpha(s(f))$, similarly for the target.

Let $\mathrm{Cat}$$\mathrm{Cat}$ be the category of small categories, then we have a faithful forgetful functor from $\mathrm{Cat}\to \mathrm{DGraph}$$\mathrm{Cat} \to \mathrm{DGraph}$.

Also, we have a free functor from the category of directed graphs to $\mathrm{Cat}$$\mathrm{Cat}$, that is, we add all the morphisms we need from the graph. It forms a free-forget adjoint.

Path Algebra

Definition. A path is a sequence of vertices $p=a_0{a}_1\dots a_n$$p = a_0 a_1 \dots a_n$ such that $s(a_{k+1})=t(a_k)$$s(a_{k+1}) = t(a_k)$.

Define $s(p)=s(a_0)$$s(p) = s(a_0)$, $t(p)=t(a_n)$$t(p) = t(a_n)$. The length of a path $l(p)=m$$l(p) = m$ if $p=a_0{a}_1\dots a_m$$p = a_0 a_1 \dots a_m$.

For each vertex, we have a trivial path $e_i$$e_i$. If $s(p)=t(p)$$s(p) = t(p)$, we say $p$$p$ is a loop.

Now we can define the path algebra of a quiver.

Definition. A path algebra of a quiver $Q$$Q$ over a field $K$$K$, denoted as $K(Q)$$K(Q)$, is such an algebra.

As a $K$$K$-vector space, it is a free $K$$K$-vector space generated by the set of all the paths on $Q$$Q$.

The product of two paths $p=a_0{a}_1\dots a_n$$p = a_0 a_1 \dots a_n$ and $p^{\prime }=b_0{b}_1\dots b_m$$p' = b_0 b_1 \dots b_m$ is defined by

$$\begin{array}{}\text{(3)}& \begin{array}{c}{p}^{\prime }\cdot p=\{\begin{array}{ll}{a}_0{a}_1\dots b_m& \text{if }t(p)=s(p^{\prime })\\ 0& \text{if }t(p)\ne s(p^{\prime })\end{array}.\end{array}\end{array}$$

and naturally extends it to the whole algebra.

Denote the free vector space of $\{p\in K(Q)\mid l(p)=n\}$$\{p \in K(Q) \mid l(p) = n\}$ as $P_n$$P_n$. It is easy to see this is a subspace of $K(Q)$$K(Q)$. Here $P_0$$P_0$ is spanned by $v_i\in Q_0$$v_i \in Q_0$.

It is easy to see this is a $(\mathbb{N},+)$$(\mathbb{N}, +)$ graded algebra, $K(Q)={\displaystyle \underset{i=0}{\overset{\mathrm{\infty }}{⨁}}{P}_n}$$K(Q) = \displaystyle \bigoplus_{i=0}^\infty P_n$. Hence we can define the Euler derivation for this algebra.

$$\begin{array}{}\text{(4)}& \mathrm{\forall }p\in P_n,d(p)=np\end{array}$$

This is a derivation since

$$\begin{array}{}\text{(5)}& d(\sum _{i\in I}{p}_i)=\sum _{i\in I}d{p}_i.\end{array}$$

Also, if $p\in P_i$$p \in P_i$ and $q\in P_j$$q \in P_j$, then $pq\in P_{i+j}=P_n$$pq \in P_{i+j} = P_n$. Then $d(pq)=npq=ipq+jpq=d(p)q+pd(q)$$d(pq) = npq = ipq + jpq = d(p)q + pd(q)$.

It is easy to see that $e_i{e}_j={\delta }_{i,j}{e}_i$$e_i e_j = \delta_{i,j} e_i$, i.e. $e_i^2=e_i$$e_i^2 = e_i$, $e_i{e}_j=0$$e_i e_j = 0$, and ${\displaystyle 1=\sum _{e_i\in Q_0}{e}_i}$$\displaystyle 1 = \sum_{e_i \in Q_0} e_i$.

Proposition. Let $Q$$Q$ be a finite quiver, then $\dim K(Q)=\mathrm{\infty }$$\dim K(Q) = \infty$ iff $Q$$Q$ has a loop.

Proof.

If $Q$$Q$ has a loop, then we could consider $p,p^2,p^3,\dots ,p^n,\dots$$p, p^2, p^3, \dots, p^n, \dots$ hence $\dim K(Q)=\mathrm{\infty }$$\dim K(Q) = \infty$.

If $Q$$Q$ has no loop, then the end vertex and starting vertex of any path are always distinct, hence there are only finitely many paths over $Q$$Q$, hence $\dim K(Q)<\mathrm{\infty }.◻$$\dim K(Q) < \infty.\quad \square$

Example of Path Algebra

Let $Q$$Q$ be a quiver such that $Q_0=\{\ast \}$$Q_0 = \{*\}$, $|Q_1|=n$$|Q_1| = n$, that is, a quiver with $n$$n$ loops and we require that each loop is not invertible. Then $K(Q)\cong K[T_1,T_2,\dots ,T_n]$$K(Q) \cong K[T_1, T_2, \dots, T_n]$.

People familiar with the fundamental group could connect this with the fundamental group of $\underset{i=1}{\overset{n}{\bigvee }}{S}^1$$\bigvee_{i=1}^n S^1$ being the free group on $\{1,2,3,\dots ,n\}$$\{1, 2, 3, \dots, n\}$.

Let $Q$$Q$ be a quiver such that

$$\begin{array}{}\text{(6)}& e_1\stackrel{{\alpha }_1}{\to }{e}_2\stackrel{{\alpha }_2}{\to }{e}_3\stackrel{{\alpha }_3}{\to }\cdots \stackrel{{\alpha }_{n-1}}{\to }{e}_n\end{array}$$

So the $s({\alpha }_i)=e_i$$s(\alpha_i) = e_i$, $t({\alpha }_i)=e_{i+1}$$t(\alpha_i) = e_{i+1}$. We could represent $e_i$$e_i$ as $E_{ii}$$E_{ii}$ and ${\alpha }_i=E_{i,i+1}$$\alpha_i = E_{i,i+1}$. Hence $K(Q)$$K(Q)$ is isomorphic to the upper triangular matrix algebra.