Normal Distribution as Orbit of Standard Normal Distribution under Affine Group Action

Let us consider the semi-direct product $A=(\mathbb{R},+)⋊({\mathbb{R}}^{+},\cdot )$$A=(\R,+)\rtimes(\R^+,\cdot)$ we represent the elements by ${\displaystyle \frac{x}{a}}+b$$\dfrac{x}{a}+b$ where $a>0$$a>0$.

Then consider the faithful group action via

$$\begin{array}{}\text{(1)}& \tau :A\hookrightarrow {\mathrm{Aut}}_{\mathrm{Met}}(L^1(\mathbb{R})),\tau ({\displaystyle \frac{x}{a}}+b)f(x)={\displaystyle \frac{1}{a}}f({\displaystyle \frac{x}{a}}+b)\end{array}$$

$\tau$$\tau$ is a group homomorphism since

$$\begin{array}{}\text{(2)}& \tau \left(({\displaystyle \frac{x}{a}}+b)\circ ({\displaystyle \frac{x}{c}}+d)\right)f(x)=\tau (\frac{x}{ac}+\frac{d}{a}+b)f(x)={\displaystyle \frac{1}{ac}}f({\displaystyle \frac{x}{ac}}+(\frac{d}{a}+b))\end{array}$$

and

$$\begin{array}{}\text{(3)}& \tau ({\displaystyle \frac{x}{a}}+b)\cdot \tau ({\displaystyle \frac{x}{c}}+d)f(x)=\tau ({\displaystyle \frac{x}{a}}+b){\displaystyle \frac{1}{c}}f({\displaystyle \frac{x}{c}}+d)={\displaystyle \frac{1}{ac}}f({\displaystyle \frac{x}{ac}}+\frac{d}{a}+b)\end{array}$$

Also, this group action will preserve norm, i.e. ${\Vert \tau ({\displaystyle \frac{x}{a}}+b)f\Vert }_1=\parallel f{\parallel }_1$$\left\|\tau\left(\dfrac{x}{a}+b\right)f\right\|_1=\|f\|_1$. Hence it is a automorphism of sphere in $L^1(\mathbb{R})$$L^1(\R)$.

It is faithful since

$$\begin{array}{}\text{(4)}& \tau ({\displaystyle \frac{x}{a}}+b)x={\displaystyle \frac{x}{a}}+b\ne {\displaystyle \frac{x}{c}}+d=\tau ({\displaystyle \frac{x}{c}}+d)x\end{array}$$

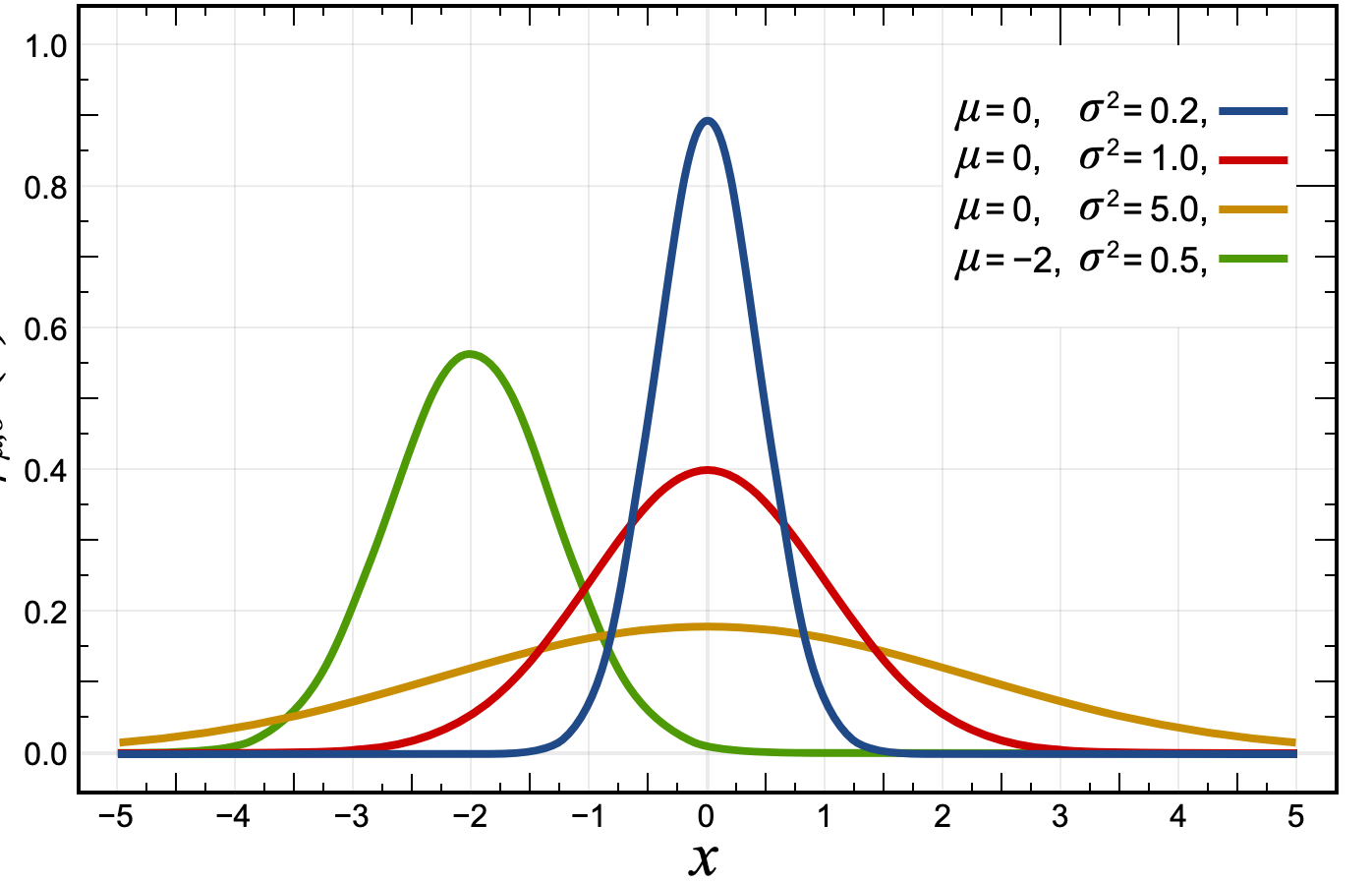
Now let us consider the probability density function of standard normal distribution or unit normal distribution.

$$\begin{array}{}\text{(5)}& f(x)={\displaystyle \frac{1}{\sqrt{2\pi }}}\exp (-{\displaystyle \frac{x^2}{2}})\in S(L^1(\mathbb{R}))=\{f\in L^1(\mathbb{R}):\parallel f{\parallel }_1=1\}\subseteq L^1(\mathbb{R})\end{array}$$

As you can see, the probability density function of normal distribution is just the orbit ${\mathcal{O}}_A(f)$$\mathcal O_A(f)$.

$$\begin{array}{}\text{(6)}& \tau (\frac{x}{a}+b)f(x)=\frac{1}{a}\cdot \frac{1}{\sqrt{2\pi }}{e}^{-\frac{(\frac{x}{a}+b{)}^2}{2}}=\frac{1}{\sqrt{2\pi a^2}}{e}^{-\frac{(x+ab{)}^2}{2a^2}}\end{array}$$

Compare it with ${\displaystyle f(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}}$$\displaystyle f(x)=\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$, we get that $a=\sigma ,\mu =-ab,b={\displaystyle \frac{-\mu }{\sigma }}$$a=\sigma,\mu=-ab,b=\dfrac{-\mu}{\sigma}$. i.e.

$$\begin{array}{}\text{(7)}& \tau \left(\frac{x-\mu }{\sigma }\right)f(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\end{array}$$

Since all the probability density function of standard normal distribution is just the orbit of ${\mathcal{O}}_A(f)$$\mathcal O_A(f)$ and given by $(6).$$(6).$​

Hence there is only one orbit of this group action, hence it is transitive action.

So the so called Normalization is just consider $g^{-1}$$g^{-1}$ acts on $g\cdot x$$g\cdot x$. It is easy to see that ${\displaystyle {\left(\frac{x-\mu }{\sigma }\right)}^{-1}=\sigma x+\mu }$$\displaystyle\left(\frac{x-\mu}{\sigma}\right)^{-1}=\sigma x+\mu$.