The Law of Quadratic Reciprocity

This blog is a polish of:

G. Zolotarev, Nouvelle démonstration de la loi de réciprocité de Legendre, Nouv. Ann. Math (2), 11 (1872), 354-362

https://marco-yuze-zheng.blogspot.com/2024/03/legendre-symbol-exact-sequence-point-of.html

We know that from Cayley's theorem, we have a injective homomorphism $i:G\hookrightarrow {\mathrm{Aut}}_{\mathrm{Set}}(G)$$i:G\hookrightarrow\mathrm{Aut}_{\mathrm{Set}}(G)$​.

Lemma 1. Let $n$$n$ be an even number, then there is an unique surjetive group homomorphism $f:\mathbb{Z}/n\mathbb{Z}\to \mathbb{Z}/2\mathbb{Z}$$f:\mathbb Z/n\mathbb Z\to\mathbb Z/2\mathbb Z$.

Proof. It follows from the ideal $(2)$$(2)$ is the only possible kernel. $◻$$\square$​

Notice that ${\mathbb{F}}_p^{\ast }\cong \mathbb{Z}/(p-1)\mathbb{Z}$$\mathbb F_p^*\cong\mathbb Z/(p-1)\mathbb Z$, we have following diagram commute.

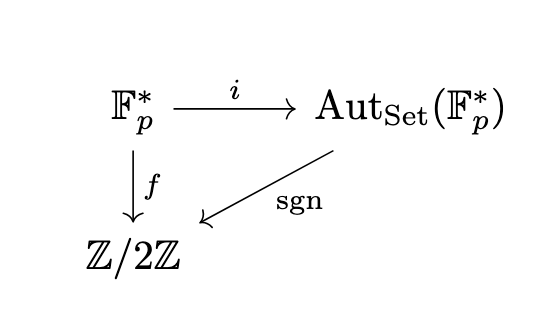
Thus we have $\left({\displaystyle \frac{q}{p}}\right)=\mathrm{sgn}(q)$$\left(\dfrac{q}{p}\right)=\mathrm{sgn}(q)$​.

The Law of Quadratic Reciprocity

Now consider $\tau :\mathbb{Z}/pq\mathbb{Z}\to \mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/q\mathbb{Z}$$\tau:\mathbb Z/pq\mathbb Z\to\mathbb Z/p\mathbb Z\times\mathbb Z/q\mathbb Z$ and $\lambda ,\alpha :\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/q\mathbb{Z}\to \mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/q\mathbb{Z}$$\lambda,\alpha:\mathbb Z/p\mathbb Z\times\mathbb Z/q\mathbb Z\to \mathbb Z/p\mathbb Z\times\mathbb Z/q\mathbb Z$

$$\begin{array}{}\text{(1)}& \tau (x)=(x,x),\lambda (a,b)=(a,a+pb),\alpha (a,b)=(qa+b,b)\end{array}$$

Now define the permutation $\phi :\mathbb{Z}/pq\mathbb{Z}\to \mathbb{Z}/pq\mathbb{Z}$$\varphi:\mathbb Z/pq\mathbb Z\to\mathbb Z/pq\mathbb Z$ by $\phi (a+pb)=qa+b$$\varphi(a+pb)=qa+b$

The key point is

$$\begin{array}{}\text{(2)}& 𝜑={𝜏}^{-1}\circ 𝛼\circ {𝜆}^{-1}\circ 𝜏\end{array}$$

Hence

$$\begin{array}{}\text{(3)}& \mathrm{sgn}(\phi )=\mathrm{sgn}(\alpha )\mathrm{sgn}(\lambda )\end{array}$$

Also,

$$\begin{array}{}\text{(4)}& \mathrm{sgn}(\alpha )=\left({\displaystyle \frac{q}{p}}\right),\mathrm{sgn}(\beta )=\left({\displaystyle \frac{p}{q}}\right)\end{array}$$

Since actually $\alpha$$\alpha$ is acting on $\mathbb{Z}/p\mathbb{Z}$$\mathbb Z/p\mathbb Z$, and equal to composition of $f_q:x⟼qx$$f_q:x\longmapsto qx$ and $g_b:x⟼x+b$$g_b:x\longmapsto x+b$.

But $\mathrm{sgn}(g_b)=\mathrm{sgn}(g_1^b)=\mathrm{sgn}(g_1{)}^b$$\mathrm{sgn}(g_b)=\mathrm{sgn}(g_1^b)=\mathrm{sgn}(g_1)^b$. But $g_1=(0,1,2,3,...,p-1)$$g_1=(0,1,2,3,...,p-1)$ hence $\mathrm{sgn}(g_1)=1$$\mathrm{sgn}(g_1)=1$.

Hence $\mathrm{sgn}(\alpha )=\mathrm{sgn}(f_q)=\left({\displaystyle \frac{q}{p}}\right)$$\mathrm{sgn}(\alpha)=\mathrm{sgn}(f_q)= \left(\dfrac{q}{p}\right)$, similarly, $\mathrm{sgn}(\beta )=\left({\displaystyle \frac{p}{q}}\right)$$\mathrm{sgn}(\beta)=\left(\dfrac{p}{q}\right)$.

Hence

$$\begin{array}{}\text{(5)}& \mathrm{sgn}(\phi )=\left({\displaystyle \frac{q}{p}}\right)\left({\displaystyle \frac{p}{q}}\right)\end{array}$$

Now let us compute $\mathrm{sgn}(\phi )$$\mathrm{sgn}(\varphi)$, i.e. we need to count the number of the inversions.

$$\begin{array}{}\text{(6)}& a_1+p{b}_1<a_2+p{b}_2\wedge q{a}_2+b_2<q{a}_1+b_1⟺a_1-a_2<p(b_2-b_1)<pq(a_1-a_2)\end{array}$$

Hence $a_1-a_2>0,a_1>a_2$$a_1-a_2>0,a_1>a_2$, and this force that $b_2>b_1$$b_2>b_1$ is the condition of inversions.

Hence the number of inversions are $\begin{array}{c}(\genfrac{}{}{0ex}{}{p}{2})(\genfrac{}{}{0ex}{}{q}{2})\end{array}$$\binom{p}{2}\binom{q}{2}\\$​, this shows that

$$\begin{array}{}\text{(7)}& \mathrm{sgn}(\phi )=(-1{)}^{{\displaystyle (\genfrac{}{}{0ex}{}{p}{2})(\genfrac{}{}{0ex}{}{q}{2})}}=(-1{)}^{{\displaystyle \frac{p(p-1)q(q-1)}{4}}}=(-1{)}^{{\displaystyle \frac{(p-1)(q-1)}{4}}}=\left({\displaystyle \frac{q}{p}}\right)\left({\displaystyle \frac{p}{q}}\right)◻\end{array}$$