Tensor–Operator Framework for Integration-by-Parts Identities and the Higher-Order Leibniz Rule

This blog rewrites my work from two years ago in a more precise way.

A good explanation for Leibniz's rule for higher derivatives is similar to the Binomial theorem(in general, multinomia theorem)

Integration by Parts and Polynomial Identities (sum and difference of the n-th powers of x and y)

Leibniz's rule for higher derivatives Integration by Parts and Polynomial Identities

Leibniz's rule for higher derivatives

Let $A=C^{\mathrm{\infty }}(\mathbb{R}),D={\displaystyle \frac{d}{dx}}$$A=C^{\infty}(\mathbb R),D=\dfrac{d}{dx}$. Define $D_1=D\otimes \mathrm{id},D_2=\mathrm{id}\otimes D:A{\otimes }_{\mathbb{R}}A\to A{\otimes }_{\mathbb{R}}A$$D_1=D\otimes\mathrm{id},D_2=\mathrm{id}\otimes D:A\otimes_\mathbb R A\to A\otimes_\mathbb R A$.

Notice that $D_1{D}_2=D\otimes D=D_2{D}_1$$D_1D_2=D\otimes D=D_2 D_1$. Now consider $m:A{\otimes }_{\mathbb{R}}A\to A,m(u\otimes v)=uv$$m:A\otimes_{\mathbb R} A\to A,m(u\otimes v)=uv$ and ${\partial }_i=m\circ D_i$$\partial_i= m\circ D_i$.

Then we have the following equations:

$${\partial }_1(u\otimes v)=u^{\prime }v,{\partial }_2(u\otimes v)=u{v}^{\prime }$$

And

$$D\circ m=m\circ (D_1+D_2)={\partial }_1+{\partial }_2$$

Proposition.

Let $T:X\to Y$$T:X\to Y$ be a morphism and $S\in \mathrm{End}(X),U\in \mathrm{End}(Y)$$S\in\mathrm{End}(X),U\in\mathrm{End}(Y)$. If $ST=TU$$ST=TU$, then $S^{n}T=T{U}^n$$S^nT=TU^n$.

Proof.

We use mathematical induction here.

Assume that $S^{n-1}T=T{U}^{n-1}$$S^{n-1}T=TU^{n-1}$, then

$$S^{n}T=S^{n-1}(ST)=(S^{n-1}T)U=T{U}^n◻$$

Corollary. Leibniz Law for Higher derivative.

$$D^n\circ m(u\otimes v)=m\circ (D_1+D_2{)}^n(u\otimes v)=m(\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})D_1^k{D}_2^{n-k}(u\otimes v))$$

i.e.

$$D^n(uv)=\left(\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})u^k{v}^{n-k}\right)◻$$

Integration by Parts and Polynomial Identities

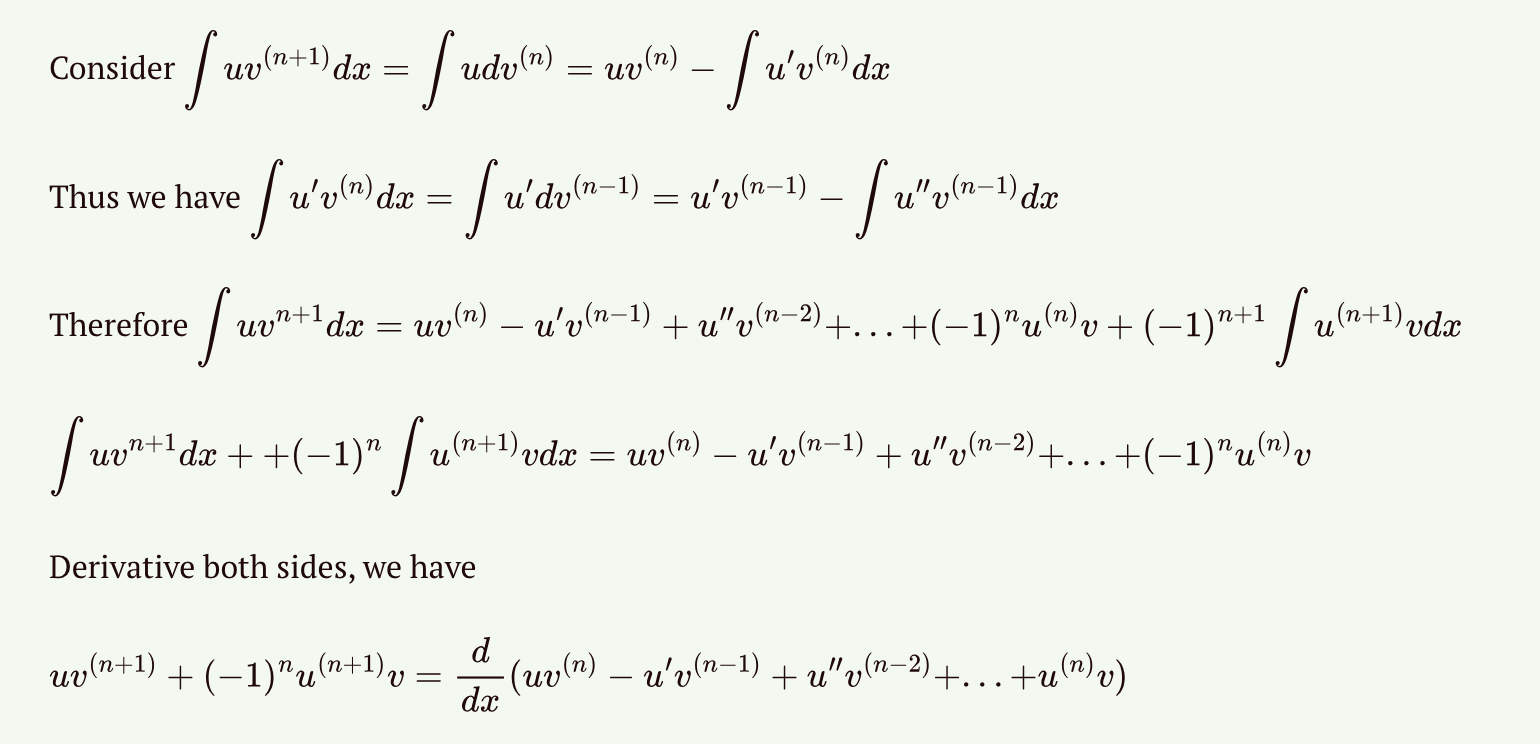
That is,

$$({\partial }_2^{n+1}+(-1{)}^{n+1}{\partial }_1^{n+1})(u\otimes v)=D\circ m(\sum _{k=0}^n(-1{)}^k{\partial }_2^k{\partial }_1^{n-k})(u\otimes v)$$

But

$$D\circ m=m\circ (D_1+D_2)={\partial }_1+{\partial }_2$$

Hence we have

$$({\partial }_2^{n+1}+(-1{)}^n{\partial }_1^{n+1})(u\otimes v)=({\partial }_2+{\partial }_1)(\sum _{k=0}^n(-1{)}^k{\partial }_2^k{\partial }_1^{n-k})(u\otimes v)$$

That is a way to see the identity

$$x^{n+1}+(-1{)}^n{y}^{n+1}=(x+y)\sum _{k=0}^n{x}^k(-y{)}^{n-k}$$