Compact Oriented Boundary‑less Surfaces as a Symmetric Monoidal Category: Genus and the Grothendieck Group

The Monoidal category structure of category of compact, oriented surfaces with no boundaryGenus as a Monoidal functor Grothendieck Group $K_0(\mathcal{C})$

 

The Monoidal category structure of category of compact, oriented surfaces with no boundary

Definition.

Let us consider the category of compact, oriented surfaces with no boundary and orientation‑preserving homeomorphisms between surfaces. Denote the category as $\mathcal{C}$$\mathcal C$.

Then we define a bifunctor $\mathrm{\#}:\mathcal{C}\times \mathcal{C}\to \mathcal{C}$$\#:\mathcal C\times\mathcal C\to\mathcal C$ , called connected sum.

On object

Remove an embedded disk $D^2$$D^2$ from each surface and glue along the resulting boundary circles:

$M\mathrm{\#}N$$M \,\#\, N$

is their connected sum, again a compact oriented surface.

On morphisms

Given

$f:M\stackrel{\cong }{\to }{M}^{\prime },g:N\stackrel{\cong }{\to }{N}^{\prime }$$f: M \xrightarrow{\cong} M',\quad g: N \xrightarrow{\cong} N'$

define

$$f\mathrm{\#}g:M\mathrm{\#}N⟶M^{\prime }\mathrm{\#}{N}^{\prime }$$

by applying f on the $M\setminus D^2$$M\setminus D^2$ part, $g$$g$ on the $N\setminus D^2$$N\setminus D^2$ part, and extending over the gluing circle.

 

One checks functoriality:

$$(g\circ f)\mathrm{\#}(g\prime \circ f\prime )=(g\circ g^{\prime })\mathrm{\#}(f\circ f^{\prime }),{\mathrm{id}}_M\mathrm{\#}{\mathrm{id}}_N=\mathrm{id}M\mathrm{\#}N.$$

The Unit Object

Take the 2‑sphere $S^2$$S^2$ as the tensor unit $I$$I$. Since

$$S^2\mathrm{\#}M\cong M\text{and}M\mathrm{\#}{S}^2\cong M$$

(via “capping off” the removed disk), $S^2$$S^2$ acts as a strict unit up to canonical homeomorphism.

The associator is:

$${\alpha }_{M,N,P}:(M\mathrm{\#}N)\mathrm{\#}P\stackrel{\cong }{\to }M\mathrm{\#}(N\mathrm{\#}P).$$

By the classification of surfaces, the two ways of performing connected sums give canonically homeomorphic surfaces; these homeomorphisms are natural in $M,N,P$$M,N,P$.

The left and right unitors as follows:

$${\lambda }_M:S^2\mathrm{\#}M\stackrel{\cong }{\to }M,{\rho }_M:M\mathrm{\#}{S}^2\stackrel{\cong }{\to }M.$$

$${\sigma }_{M,N}:M\mathrm{\#}N\stackrel{\cong }{\to }N\mathrm{\#}M$$

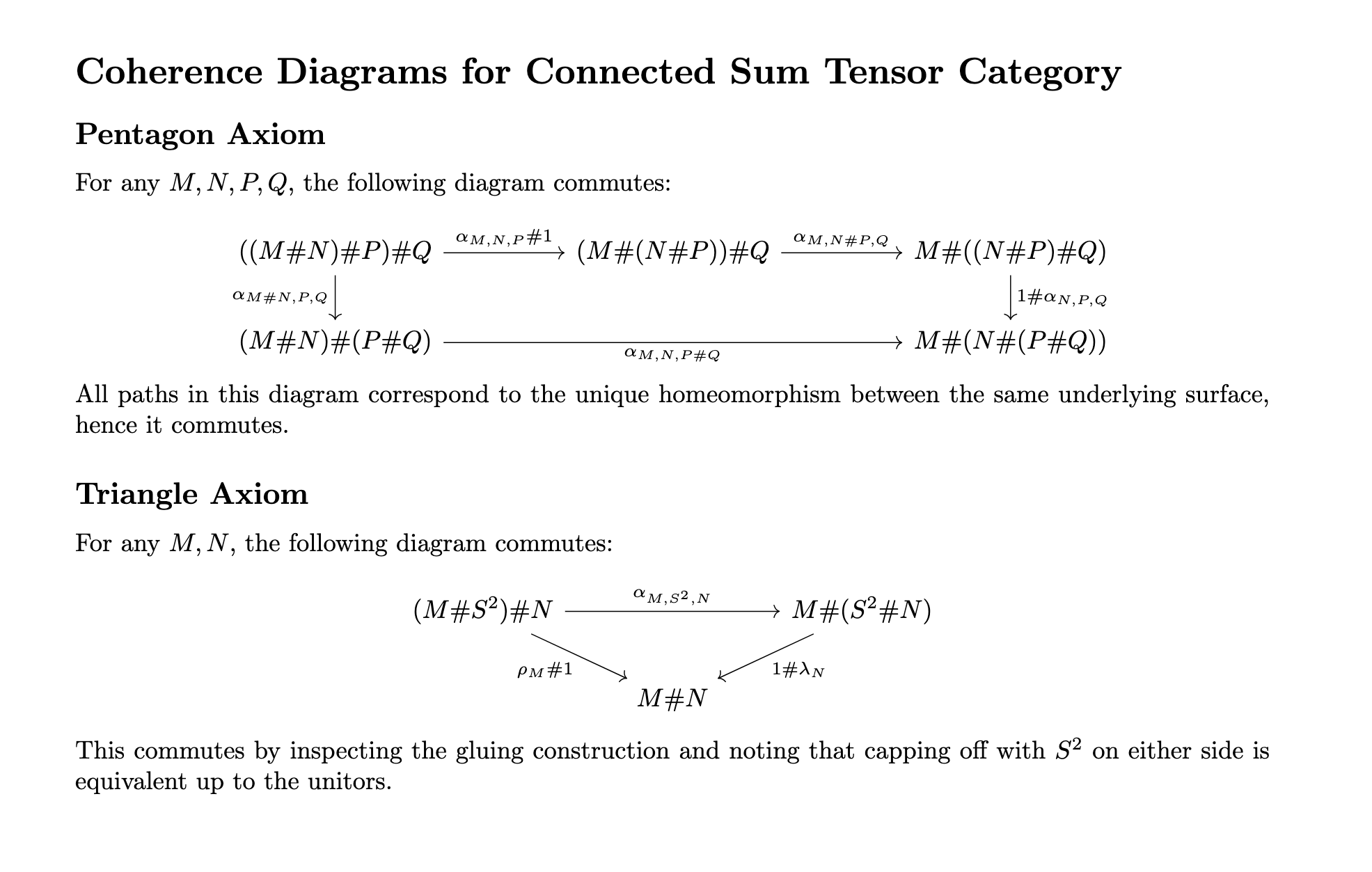
by interchanging the two chosen disks before gluing. These $({\sigma }_{M,N})$$(\sigma_{M,N})$ satisfy the usual hexagon axioms, making $\mathcal{C}$$\mathcal C$ become a symmetric monoidal.

Genus as a Monoidal functor

We view the category of compact oriented boundaryless surfaces and the discrete category on as monoidal categories, and then define the genus functor.

View genus as a functor

 

$$g:(\mathcal{C},\mathrm{\#},S^2)⟶(\mathbb{N},+,0),$$

• the codomain is A strict monoidal category

  • Objects: natural numbers .

  • Morphisms: only identities .

  • Tensor product: $+$$+$ .

  • Unit: $0$$0$

It maps a surface to its genus, and we have $g(M\mathrm{\#}N)=g(M)+g(N)$$g(M\# N)=g(M)+g(N)$.

By the classification theorem of compact surface, we know that $M\cong N⟺g(M)=g(N)$$M\cong N\iff g(M)=g(N)$.

Hence we can see that the Grothendieck group of $\mathcal{C}$$\mathcal C$ is just $\mathbb{Z}$$\mathbb Z$.

Grothendieck Group $K_0(\mathcal{C})$$K_0(\mathcal{C})$

The Grothendieck group of the monoidal category (\mathcal{C}) is the group completion of the commutative monoid of isomorphism classes of objects under (#).

• Monoid of isomorphism classes $\mathrm{Iso}(\mathcal{C})=\{[M]\mid M\in \mathrm{Ob}(\mathcal{C})\},$$\mathrm{Iso}(\mathcal{C}) = \{[M]\mid M\in\mathrm{Ob}(\mathcal{C})\},$ $[M]+[N]:=[M\mathrm{\#}N]$$[M]+[N]:=[M\# N]$ By surface classification, $\mathrm{Iso}(\mathcal{C})\cong (\mathbb{N},+,0),[M]⟼\mathrm{genus}(M).$$\mathrm{Iso}(\mathcal{C}) \;\cong\; (\mathbb{N},+,\;0), \quad [M]\;\longmapsto\;\mathrm{genus}(M).$

• Group completion

  $$K_0(\mathcal{C})=\mathrm{Gr}(\mathrm{Iso}(\mathcal{C}))\cong \mathrm{Gr}(\mathbb{N})\cong \mathbb{Z},$$

Readers should compare it with the Grothendieck group of Category of finite dimensional vector space over a field.