The first example
Let be a field extension, .
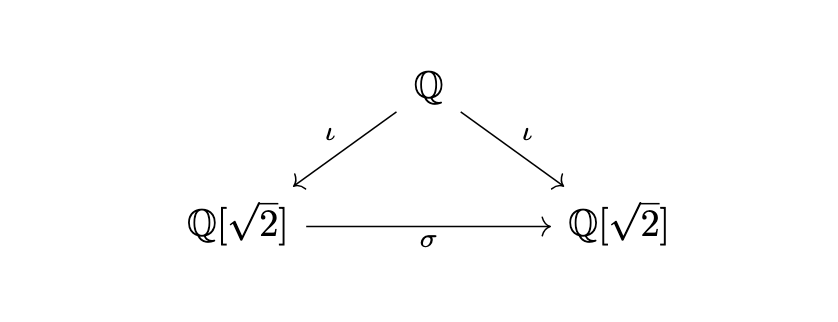
We could induce a ring homomorphism
and act the spectrum functor both sides
Consider ,
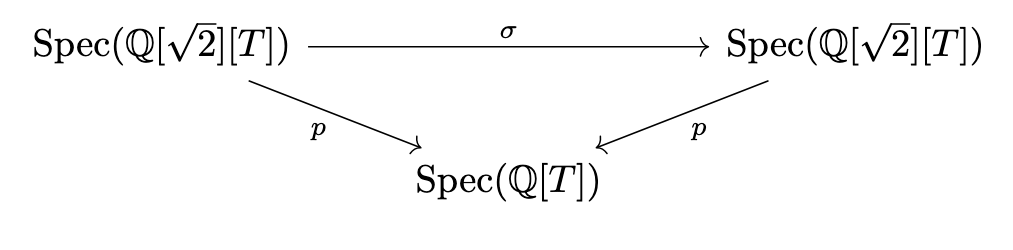
and we could view the roots of irreducible polynomial as fiber at .
Let , then , hence as well.
This is a geometric interpretation of the fact that the Galois group permutes the roots of .
In this case, correspond to the orbit of under .
Fiber functor.
Consider the slice category . Let be a point in , then we can define a fiber functor as follows:
For a morphism
We have
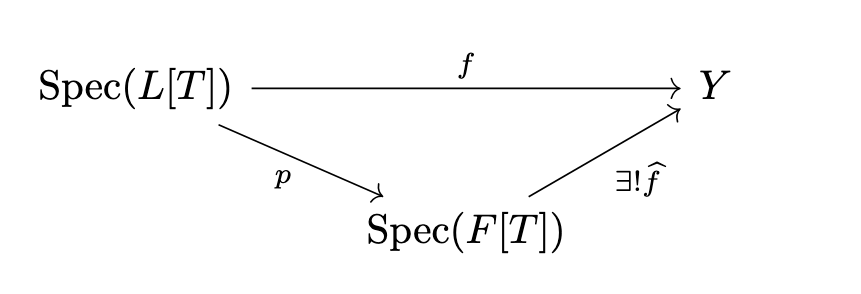
Splitting field
Let be an irreducible polynomial and be the splitting field of , and is separateble in .
Then we could consider the following diagram:
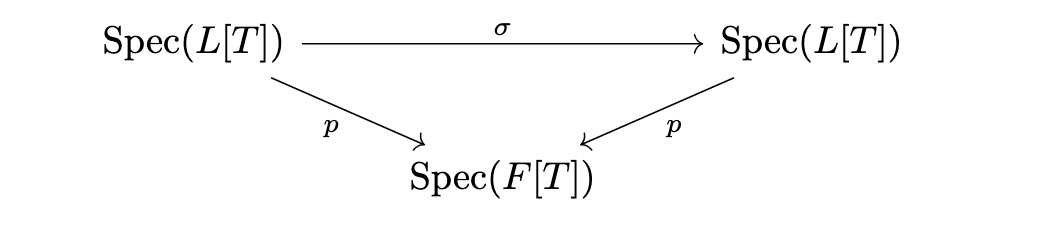
Again, for a point , the fiber correspond to the roots of in .
The fiber functor shows that why the Galois group permute the roots of via .
Orbit Space
Let be a group and let acts on via . We denote that to be the space of orbit of this group action.
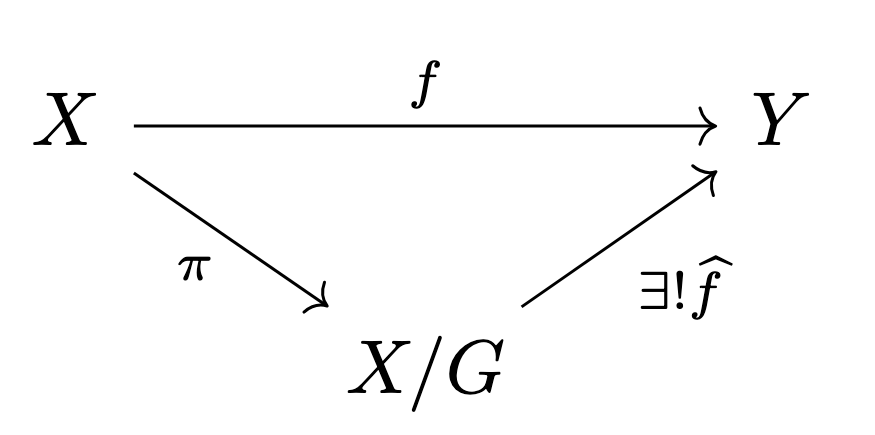
For all the invariant function, i.e. , we have an unique function such that
Now think about the splitting field of again.
Consider the orbit space
We know that the Galois group act transitive at the roots of since is irreducible.
Then a irreducible polynomial split in iff .
Hence the orbit space
So the Galois Group ''glue them back''.
The can be viewed as the projection from to .
Hence we get the universal property of the affine scheme :



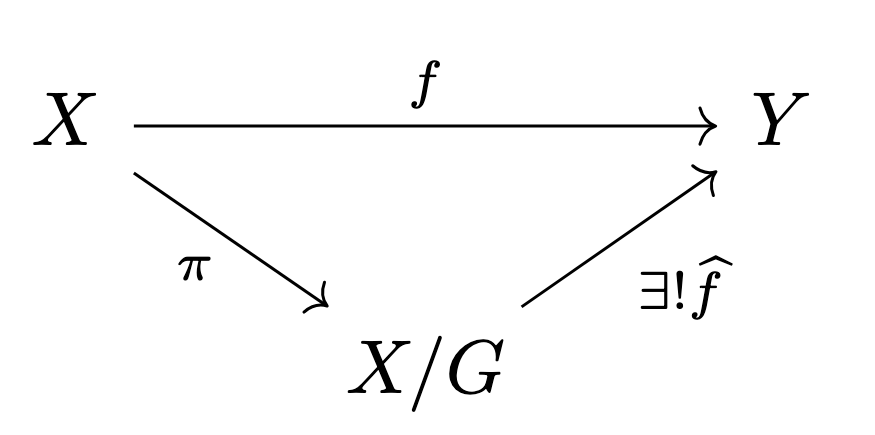




No comments:
Post a Comment