
I would like to provide an approach for from the homological algebra perspective.
The theorem we will use was proved by Kuang-wei Yang in the paper Completion of Normed Linear Spaces.
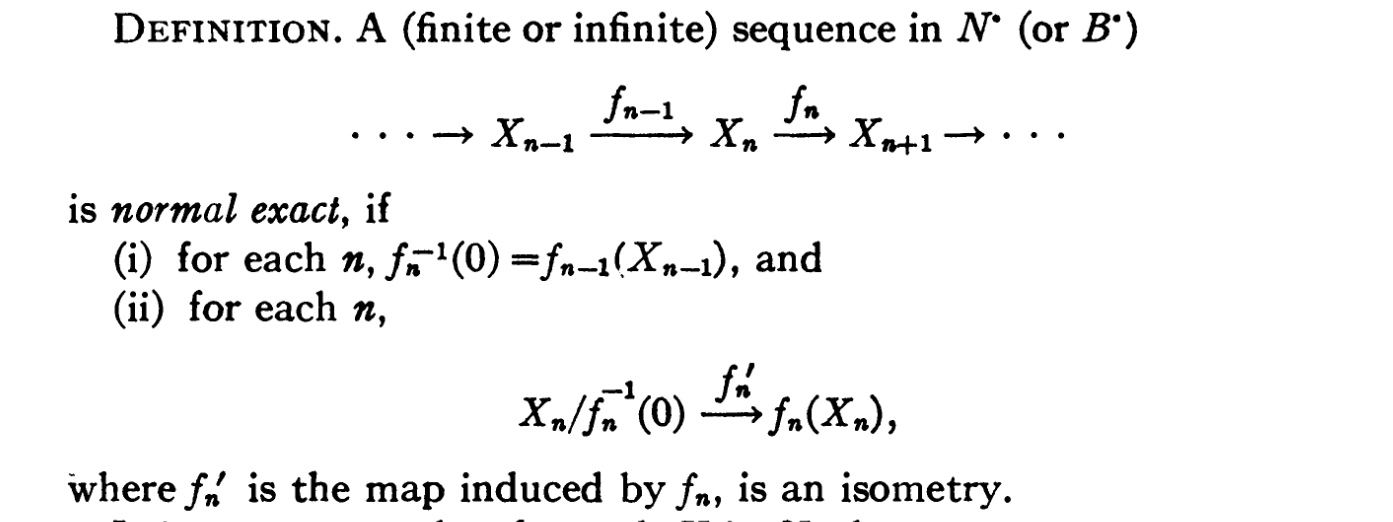
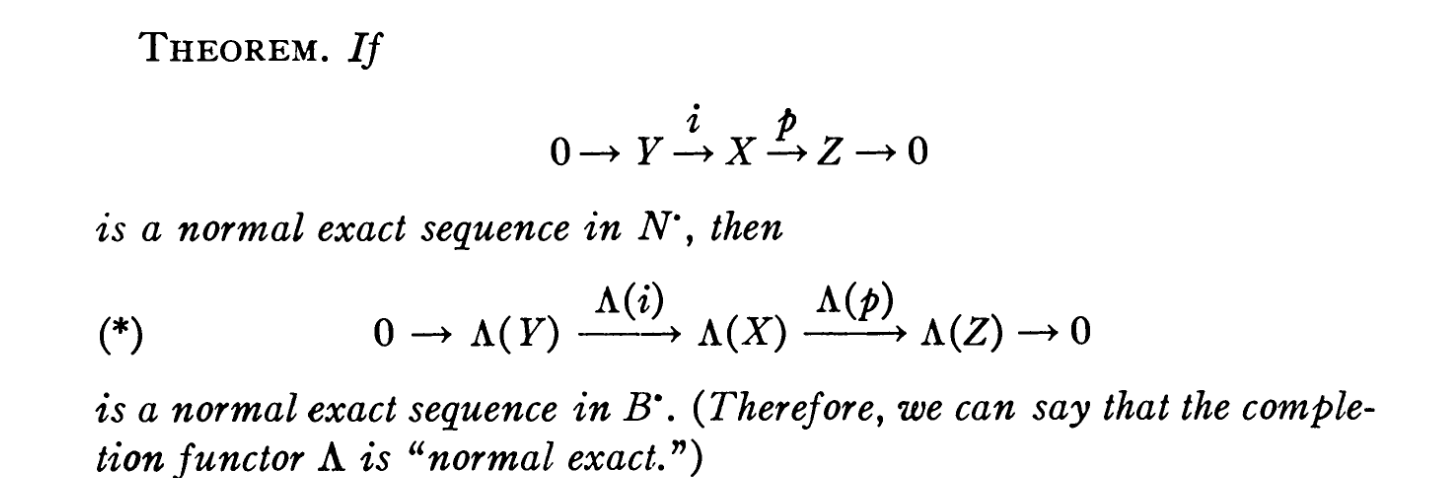
Here is the category of normed linear space with contraction maps, and is the category of Banach space with contraction maps.
Now apply the theorem above, let , we have the following normal exact sequence
Remark. It is easy to see that it is exact, for normal, consider
Apply the complement functor, we have the following normal exact sequence
Here , hence .

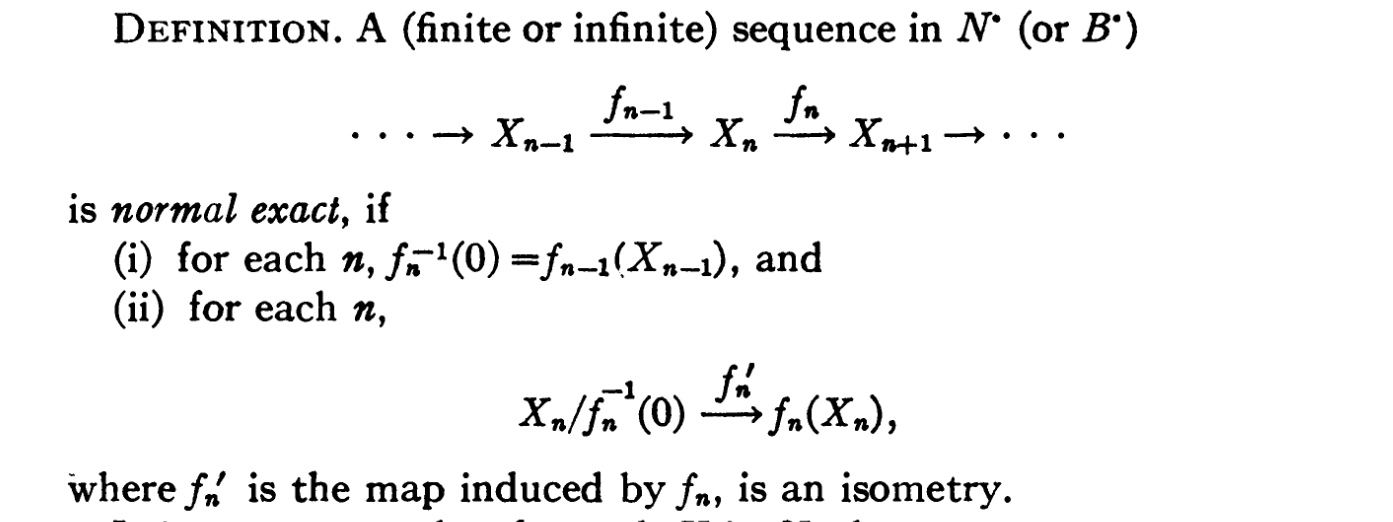
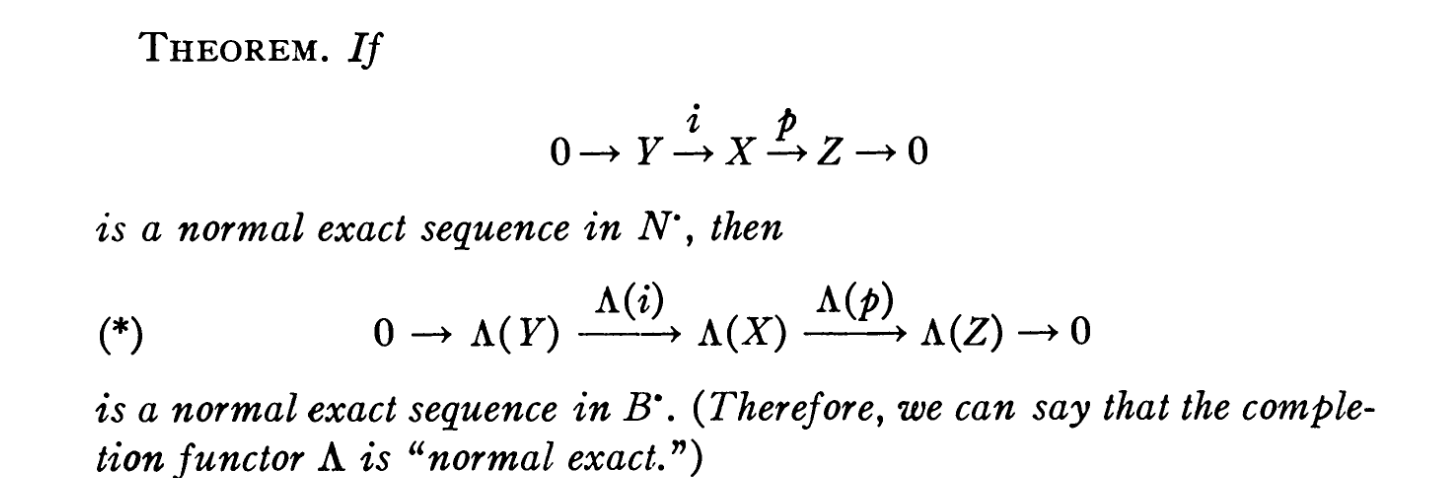



No comments:
Post a Comment