For the reason we consider
Let us define a functor
Then we claim that
Proof. Let
For any morphism
Easy to see that
Corollary.
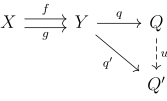
In particular, we have
For the reason we consider
Let us define a functor
Then we claim that
Proof. Let
For any morphism
Easy to see that
Corollary.
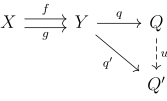
In particular, we have
 Hello, everyone! My name is Marco, and as a passionate mathematics student, I have built this blog to share some interesting ideas that come to my mind,and notes for some books I read. I'm excited to connect with others to share my love for this subject, and I hope my posts will inspire and entertain you. Thank you for visiting, and I look forward to your feedback and comments!
Hello, everyone! My name is Marco, and as a passionate mathematics student, I have built this blog to share some interesting ideas that come to my mind,and notes for some books I read. I'm excited to connect with others to share my love for this subject, and I hope my posts will inspire and entertain you. Thank you for visiting, and I look forward to your feedback and comments!
No comments:
Post a Comment