The Universal Property of Quotient Groups Through Coequalizers and Categorical Definition of Normal Closures

Let $X,Y$$X,Y$ be two groups, and $f:X\to Y$$f:X\to Y$ be a group homomorphism, let us consider $\mathrm{cokernel}(f):=\mathrm{Coeq}(f,0)$$\mathrm{cokernel}(f):=\mathrm{Coeq}(f,0)$.

Here is the definition of coequalizer

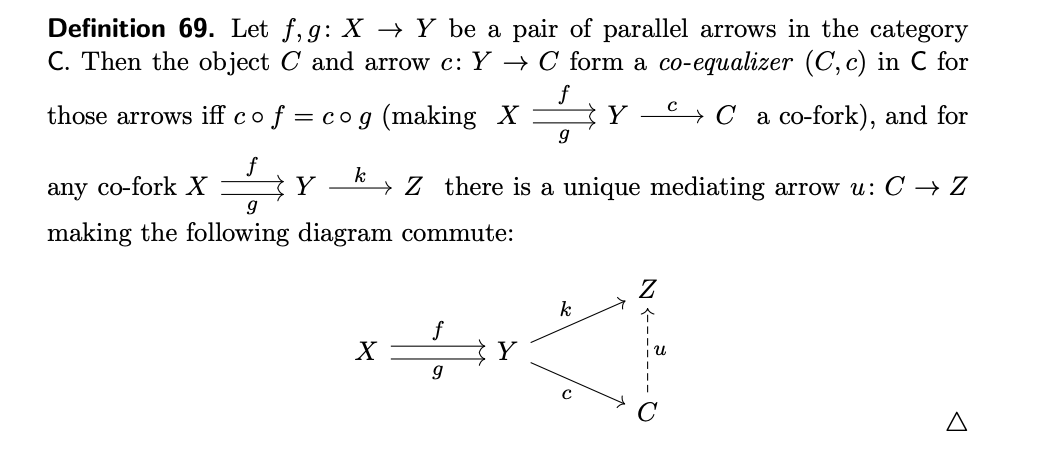
Let $g$$g$ be the zero map, i.e. $g:X\to 0\to Y$$g:X\to0\to Y$.

In particular, suppose $X$$X$ is a normal subgroup of $Y$$Y$ and $f$$f$ be the inclusion map, then $\mathrm{cokernel}(f)\cong (X/Y,\pi )$$\mathrm{cokernel}(f)\cong(X/Y,\pi)$.

That is the universal property of quotient group. i.e. Every time you have $k\circ f=k\circ 0=0$$k\circ f=k\circ 0=0$, i.e. $N\subseteq \ker (k)$$N\subseteq\mathrm{ker}(k)$

there exists a unique $u$$u$, such that $k=u\circ c$$k=u\circ c$.

If $X$$X$ is not a normal subgroup of $Y$$Y$, then the normal closure of $X$$X$, denote as $N(X)$$N(X)$ is defined to be the kernel of the cokernel map.

$$N(X):=\ker (\mathrm{cokernel})(f)=\ker (q)=\mathrm{Eq}(q,0)$$

By the universal property of equalizer, there exists a unique group homomorphism $\iota :X\to N(X)$$\iota:X \to N(X)$.

Since $\ker (q):N(X)\to Y$$\mathrm{ker}(q):N(X)\to Y$ is mono, $f:X\to Y$$f:X\to Y$ is mono and $f=\ker (q)\circ \iota$$f=\mathrm{ker}(q)\circ\iota$, hence $\iota$$\iota$ is mono as well. i.e. $X$$X$ is a subobject of $N(X)$$N(X)$.

Remark.

If $f,g$$f,g$ are mono and $f=gh$$f=gh$, then $h$$h$ is mono as well. Since if $h\circ i=h\circ j$$h\circ i=h\circ j$, then $g\circ h\circ i=g\circ h\circ j=f\circ i=f\circ j⟹i=j$$g\circ h\circ i=g\circ h\circ j=f\circ i=f\circ j\implies i=j$.