Characteristic of Ring as a functor

Proposition. $\mathbb{Z}$$\mathbb Z$ is the initial object of $\mathrm{Ring}$$\mathrm{Ring}$.

Proof. We need to show that for any ring $R$$R$, there exists a unique ring homomorphism $f_R:\mathbb{Z}\to R$$f_R:\mathbb Z\to R$.

The unique arrow $f_R:\mathbb{Z}\to R$$f_R:\mathbb Z\to R$ is given by $1⟼1_R$$1\longmapsto 1_R$, hence $f(n)=n\cdot f(1)=n\cdot 1_R$$f(n)=n\cdot f(1)=n\cdot1_R$.

Easy to see that $f$$f$ is a ring homomorphism. To see it is the only ring homomorphism, notice that a ring homomorphism has to map $1$$1$ to $1_R$$1_R$. $◻$$\square$​

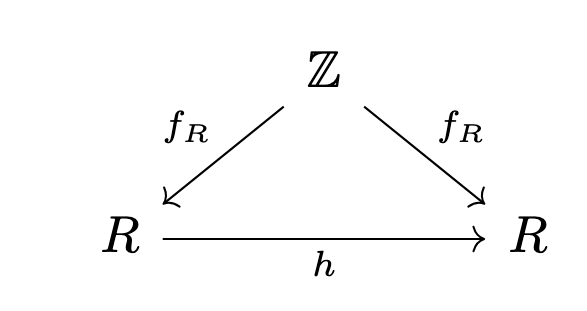
Hence we could view $\mathrm{Ring}$$\mathrm{Ring}$ as $\mathbb{Z}-\mathrm{Alg}$$\mathbb Z-\mathrm{Alg}$​.(No worries if you have no idea about $R-\mathrm{Alg}$$R-\mathrm{Alg}$)

The universal property tells us that any ring homomorphism $h:R\to R$$h:R\to R$ has to fix every $a\in f_R(\mathbb{Z})$$a\in f_R(\mathbb Z)$ since the diagram is commutes.

Application. Fermat's little theorem

Let $R=\mathbb{Z}/p\mathbb{Z}$$R=\mathbb Z/p\mathbb Z$, hence $f_R={\pi }_p$$f_R=\pi_p$ is the quotient map. Notice that ${\pi }_p(\mathbb{Z})=\mathbb{Z}/p\mathbb{Z}$$\pi_p(\mathbb Z)=\mathbb Z/p\mathbb Z$, hence for any ring endomorphism of $\mathbb{Z}/p\mathbb{Z}$$\mathbb Z/p\mathbb Z$, we have $h(n)=n\in \mathbb{Z}/p\mathbb{Z}$$h(n)=n\in\mathbb Z/p\mathbb Z$. Hence the only ring endmorphism of $\mathbb{Z}/p\mathbb{Z}$$\mathbb Z/p\mathbb Z$ is $\mathrm{id}$$\mathrm{id}$.

Notice that the Frobenius endomorphism $F:x⟼x^p$$F:x\longmapsto x^p$ is a ring endomorphism of $\mathbb{Z}/p\mathbb{Z}$$\mathbb Z/p\mathbb Z$, hence it has to be $\mathrm{id}$$\mathrm{id}$.

Hence we have $F(x)=x^p=\mathrm{id}(x)=x\in \mathbb{Z}/p\mathbb{Z}$$F(x)=x^p=\mathrm{id}(x)=x\in\mathbb Z/p\mathbb Z$. i.e.

$$\begin{array}{}\text{(1)}& x^p\equiv x\mathrm{mod}p\end{array}$$

Definition.

The characteristic of $R$$R$ is defined by the kernel of $f_R$$f_R$. If $\ker f_R=m\mathbb{Z}$$\mathrm{ker} f_R=m\mathbb Z$, then the characteristic of $R$$R$ , $\mathrm{ch}(R)$$\mathrm{ch}(R)$ is $m$$m$.

But it is too boring and not useful enough. Let us define the characteristic functor, $\mathcal{ch}:\mathrm{Ring}\to \mathrm{Ring}$$\mathscr{ch}:\mathrm{Ring}\to\mathrm{Ring}$.

For a ring $R$$R$ with $ch(R)=m$$ch(R)=m$, $\mathcal{ch}(R)=\mathbb{Z}/m\mathbb{Z}$$\mathscr{ch}(R)=\mathbb Z/m\mathbb Z$. For $g:R\to S$$g:R\to S$ with $\mathrm{ch}(R)=m,\mathrm{ch}(S)=n$$\mathrm{ch}(R)=m,\mathrm{ch}(S)=n$, $\mathcal{ch}(g):\mathbb{Z}/m\mathbb{Z}\to \mathbb{Z}/n\mathbb{Z}$$\mathscr{ch}(g):\mathbb Z/m\mathbb Z\to\mathbb Z/n\mathbb Z$.

Easy to see that this is a functor. It tells us that if $\mathcal{ch}(S)$$\mathscr{ch}(S)$ is not a factor of $\mathcal{ch}(R)$$\mathscr{ch}(R)$, then there is no ring homomorphism from $R$$R$ to $S$$S$.