Galois Connection: The Initial One and Its Application to Hilbert's Nullstellensatz

We already talk about lots of Galois Connections

Math Essays: Galois Connection in various branches (marco-yuze-zheng.blogspot.com)

Math Essays: An example of Galois Connection in module theory (marco-yuze-zheng.blogspot.com)

Math Essays: Categorical Logic 1. disjuction, conjuction, implies, quantifer as adjoint. (marco-yuze-zheng.blogspot.com)

However, we have not talk about the initial one! The Galois Connection in algebraic Galois theory!

In this essay, we will deal with the Galois Connection between subsetes of $\mathrm{Gal}(K/L)$$\mathrm{Gal}(K/L)$ and intermediate field.

The coslice category of field extension and Galois GroupGalois Connection in Algebraic Galois theory Galois Connection, redefined.Closure operator and Galois ConnectionFrom Galois connection to Closure and Interior operator.From Closure operator to Galois Connection.Basic result of Galois ConnectionAnother example of Galois Connection.Appendix: Using Galois connection to prove Hilbert's Nullstellensatz

The coslice category of field extension and Galois Group

In category of field, the morphism is field extension since the only proper ideal of a field is $0$$0$.

Hence if we have a field $L$$L$, we could consider the coslice category $L/\mathrm{Field}$$L/\mathrm{Field}$.

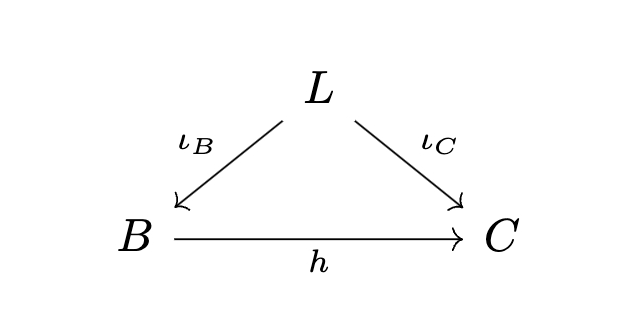
Here the object is ${\iota }_B:L\to B$$\iota_B:L\to B$, the morphism is such a $h_{\ast }({\iota }_B)={\iota }_C$$h_*(\iota_B)=\iota_C$​.

In particular, we are interested in the automorphism of a field extension from $L$$L$.

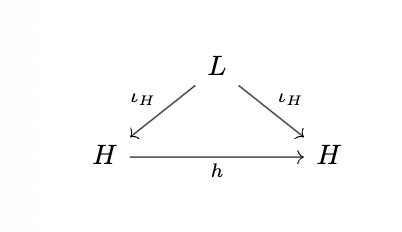
Definition. The Galois Group of a field extension is defined as $\mathrm{Gal}(H/L):={\mathrm{Aut}}_{L/\mathrm{Field}}(H/L)$$\mathrm{Gal}(H/L):=\mathrm{Aut}_{L/\mathrm{Field}}(H/L)$.

This essay will consider the relation between the subset of $\mathrm{Gal}(K/L)$$\mathrm{Gal}(K/L)$ and the intermediate field $L\subseteq M\subseteq K.$$L\subseteq M\subseteq K.$

Definition. Let $S\subseteq \mathrm{Gal}(K/L)$$S\subseteq\mathrm{Gal}(K/L)$ be a subset, define:

$$\begin{array}{}\text{(1)}& F(S):=\{a\in K|\sigma (a)=a,\mathrm{\forall }\sigma \in S\}\end{array}$$

Obviously $F(S)$$F(S)$ is a subfield of $K$$K$​, and $L\subseteq F(S)\subseteq K$$L\subseteq F(S)\subseteq K$. Easy to see that if $S\subseteq S^{\prime }$$S\subseteq S'$ then $F(S^{\prime })\subseteq F(S)$$F(S')\subseteq F(S)$.

Similarly, For a intermediate field $M$$M$ we could define:

$$\begin{array}{}\text{(2)}& G(M):=\mathrm{Gal}(K/M)\end{array}$$

Easy to see that

$$\begin{array}{}\text{(3)}& M\subseteq M^{\prime }⟹G(M^{\prime })\subseteq G(M)\end{array}$$

Galois Connection in Algebraic Galois theory

Lemma. If $S\subseteq \mathrm{Gal}(K/L)$$S\subseteq\mathrm{Gal}(K/L)$, then $S\subseteq \mathrm{Gal}(K/F(S))=GF(S)$$S\subseteq\mathrm{Gal}(K/F(S))=GF(S)$.

Proof. By definition, $GF(S)$$GF(S)$ consists of all the automorphism of $K$$K$ fixed $F(S)$$F(S)$, hence $S\subseteq GF(S).◻$$S\subseteq GF(S).\quad\square$

Lemma. $FG(M)\supseteq M$$FG(M)\supseteq M$.

Proof. By definition, $G(M)=\mathrm{Gal}(K/M)$$G(M)=\mathrm{Gal}(K/M)$ and $FG(M)$$FG(M)$ is the subfield fixed by $\mathrm{Gal}(K/M)$$\mathrm{Gal}(K/M)$.

Since $\mathrm{Gal}(K/M)$$\mathrm{Gal}(K/M)$ is all the automorphism of $K$$K$ that fixed $M$$M$, $FG(M)\supseteq M.◻$$FG(M)\supseteq M.\quad\square$​

Proposition. Galois Connection between subset of $\mathrm{Gal}(K/L)$$\mathrm{Gal}(K/L)$ and $L\subseteq M\subseteq K$$L\subseteq M\subseteq K$.

$$\begin{array}{}\text{(4)}& F(S)\supseteq M⟺S\subseteq G(M)\end{array}$$

Proof.

$⟹$$\implies$.

$F(S)\supseteq M⟹GF(S)\subseteq G(M)$$F(S)\supseteq M\implies GF(S)\subseteq G(M)$. According to the lemma, $S\subseteq GF(S)\subseteq G(M).$$S\subseteq GF(S)\subseteq G(M).$

$⟸$$\Longleftarrow$.

$S\subseteq G(M)⟹F(S)\supseteq FG(M).$$S\subseteq G(M)\implies F(S)\supseteq FG(M).$ According to the lemma, $F(S)\supseteq FG(M)\supseteq M.◻$$F(S)\supseteq FG(M)\supseteq M.\quad\square$

Corollary.

By the property of Galois Connecton, if $f(a)\le b⟺a\le g(b)$$f(a)\le b\iff a\le g(b)$. Then

$$\begin{array}{}\text{(5)}& fgf=f,gfg=g\end{array}$$

See Math Essays: Galois Connection in various branches (marco-yuze-zheng.blogspot.com)

There exists a poset isomorphism $\mathrm{Im}(f)\cong \mathrm{Im}(g)$$\mathrm{Im}(f)\cong\mathrm{Im}(g)$.

$$\begin{array}{}\text{(6)}& g:\mathrm{Im}(f)\to \mathrm{Im}(g),f(a)⟼gf(a),f:\mathrm{Im}(g)\to \mathrm{Im}(f),g(b)⟼fg(b)\end{array}$$

Since $fgf(a)=f(a)$$fgf(a)=f(a)$, $fg={\mathrm{Id}}_{\mathrm{Im}(f)}$$fg=\mathrm{Id}_{\mathrm{Im}(f)}$. Similarly, $gfg(b)=g(b)⟹gf={\mathrm{Id}}_{\mathrm{Im}(g)}$$gfg(b)=g(b)\implies gf=\mathrm{Id}_{\mathrm{Im}(g)}$.

Hence if $M=F(S)$$M=F(S)$, then $FGF(S)=F(S)=M$$FGF(S)=F(S)=M$. Similarly, if $S=G(M)$$S=G(M)$, then $GFG(M)=G(M)=S.$$GFG(M)=G(M)=S.$

Hence there exists a isomorphism between the set of $F(S)$$F(S)$ and $G(M)$$G(M)$.

Galois Connection, redefined.

Proposition. Let $f:L\to P,g:P\to L$$f:L\to P,g:P\to L$ be two monotone map between poset.

Then $f$$f$ and $g$$g$ form a pair of Galois Connection iff ${\mathrm{id}}_L\le gf,fg\le {\mathrm{id}}_P$$\mathrm{id}_L\le g f,fg\le\mathrm{id}_{P}$​.

Proof.

Assume that ${\mathrm{id}}_L\le gf,fg\le {\mathrm{id}}_P$$\mathrm{id}_L\le g f,fg\le\mathrm{id}_{P}$,

then $f(a)\le b⟹gf(a)\le g(b)$$f(a)\le b\implies gf(a)\le g(b)$. Since ${\mathrm{id}}_L\le gf$$\mathrm{id}_L\le gf$, $a\le gf(a)\le g(b),a\le g(b)$$a\le gf(a)\le g(b),a\le g(b)$.

Similarly, $a\le g(b)⟹f(a)\le fg(b)\le b,f(a)\le b$$a\le g(b)\implies f(a)\le fg(b)\le b,f(a)\le b$​. Hence we have

$$\begin{array}{}\text{(7)}& [{\mathrm{id}}_L\le gf,fg\le {\mathrm{id}}_P]⟹[f(a)\le b⟺a\le g(b)]\end{array}$$

Another direction was already proved in Math Essays: Galois Connection in various branches (marco-yuze-zheng.blogspot.com). $◻$$\square$

Closure operator and Galois Connection

Let $(L,\le )$$(L,\le)$ be a poset, then a closure operator on $L$$L$ is defined as

$$\begin{array}{}\text{(8)}& x\le c(x),x\le y⟹c(x)\le c(y),c(c(x))=c(x)\end{array}$$

By duality, we could define a interior operator as

$$\begin{array}{}\text{(9)}& i(x)\le x,x\le y⟹i(x)\le i(y),i(i(x))=i(x)\end{array}$$

Let $(L,\wedge )$$(L,\wedge)$ be a complete semi-lattice and $sup(L)$$\sup(L)$ exists. Let $(S,\wedge )$$(S,\wedge)$ be a semi-latticeand $sup(S)$$\sup(S)$ exists.

Let $\iota :(L,\wedge )\to (S,\wedge )$$\iota:(L,\wedge)\to (S,\wedge)$ is a faithful embedding and $sup(L)=sup(S)$$\sup(L)=\sup(S)$.

Then for $s\in S$$s\in S$, define $c(s)=\iota (inf\{x\in L|\iota (x)\ge s\})$$c(s)=\iota(\inf\{x\in L|\iota(x)\ge s\})$​​, easy to see that this form a closure operator.

Similarly, you can use this way to get an interior operator.

From Galois connection to Closure and Interior operator.

As you can see, for a pair of Galois connection $f(a)\le b⟺a\le g(b)$$f(a)\le b\iff a\le g(b)$ between $P,L$$P,L$, we have

$$\begin{array}{}\text{(10)}& f(x)\le f(x)⟹x\le gf(x),x\le y⟹gf(x)\le gf(y),gfgf(x)=gf(x)\end{array}$$

Hence $gf:P\to P$$gf:P\to P$ is a closure operator on $P.$$P.$ Similarly, $fg:L\to L$$fg:L\to L$ is an interior operator on $L$$L$​​.

From Closure operator to Galois Connection.

Proposition. Let $(L,\le )$$(L,\le)$ be a poset, and $(c(L),\le )$$(c(L),\le)$ be the image of $c$$c$, where $c$$c$ is a closure operator.

Then $c(x)\le y⟺x\le \iota (y)$$c(x)\le y\iff x\le \iota(y)$, here $i:c(L)\to L,\iota (y)=y$$i:c(L)\to L,\iota(y)=y$​.

Proof. $c(x)\le y⟹x\le \iota (y)$$c(x)\le y\implies x\le \iota(y)$ is obviously since $x\le c(x)$$x\le c(x)$. If $x\le \iota (y)$$x\le \iota(y)$, then $c(x)\le c(\iota (y))=\iota (y)=y.$$c(x)\le c(\iota(y))=\iota(y)=y.$​

Similarly, we have $\iota (x)\le y⟺x\le i(y)$$\iota(x)\le y\iff x\le i (y)$. Between​ $(i(L),\le )$$(i(L),\le)$ and $(L,\le )$$(L,\le)$.

Basic result of Galois Connection

Proposition.

If there exist a pair of Galois Connection $F⊣G$$F\dashv G$, $(C,⪯),(D,\le )$$(C,\preceq),(D,\le)$ and $H⊣K,(D,\le ),(E,\subseteq )$$H\dashv K,(D,\le),(E,\subseteq)$ , then we get

$$\begin{array}{}\text{(11)}& HF⊣GK,(C,⪯),(E,\subseteq )\end{array}$$

Proof.

The idea is consider $F:C\to D$$F:C\to D$ and $K:E\to D$$K:E\to D$.

Take any $c\in C$$c\in C$ and $e\in E$$e\in E$ we have $F(c)\le K(e)⟺c⪯GK(e)$$F(c)\le K(e)\iff c\preceq GK(e)$ by $F⊣G$$F\dashv G$.

Similarly we have $F(c)\le K(e)⟺HF(c)\subseteq e$$F(c)\le K(e)\iff HF(c)\subseteq e$. i.e.

$$\begin{array}{}\text{(12)}& HF(c)\subseteq e⟺c⪯GK(e)◻\end{array}$$

Proposition.

If $F⊣G$$F\dashv G$ is a pair of Galois connection between $(C,⪯),(D,\le )$$(C,\preceq),(D,\le)$, then

$†.Gd=sup\{c\in C|Fc\le d\}$$\dagger.Gd=\sup\{c\in C|Fc\le d\}$​

$†.$$\dagger.$ $Fc=inf\{d\in D|c⪯Gd\}$$Fc=\inf\{d\in D|c\preceq Gd\}$

Proof.

By definition of Galois connection, we have $Fc\le d⟺c⪯Gd$$Fc\le d\iff c\preceq Gd$.

Hence we have $Gd$$Gd$ is an upper bound of $\{c\in C|Fc\le d\}$$\{c\in C|Fc\le d\}$. But also, $FGd\le d$$FGd\le d$, hence $Gd\in \{c\in C|Fc\le d\}$$Gd\in\{c\in C|Fc\le d\}$.

Therefore, $Gd$$Gd$ is both upper bound and a member of $\{c\in C|Fc\le d\}$$\{c\in C|Fc\le d\}$. Hence $Gd$$Gd$ is the least upper bound.

Similarly, $c⪯Gd⟺Fc\le d$$c\preceq Gd\iff Fc\le d$ , hence we have $Fc$$Fc$ is a lower bound of $\{d\in D|c⪯Gd\}$$\{d\in D| c\preceq Gd\}$.

To see $Fc$$Fc$ is the greatest lower bound, consider $c⪯GFc$$c\preceq GFc$, hence $Fc\in \{d\in D|c⪯Gd\}.$$Fc\in\{d\in D|c\preceq Gd\}.$

Therefore, $Fc$$Fc$ is both lower bound and a member of $\{d\in D|c⪯Gd\}.$$\{d\in D|c\preceq Gd\}.$ $◻$$\square$

Another example of Galois Connection.

Let $(L,\le )$$(L,\le)$ be a partial order set. Let $(P(L),\subseteq )$$(P(L),\subseteq)$ be the power set of $L$$L$.

For any $S\subseteq L$$S\subseteq L$, define $S^u$$S^u$ be the set of upper bound of $S$$S$, $S^l$$S^l$ be the set of lower bound of $S$$S$.

$$\begin{array}{}\text{(13)}& S^u:=\{x\in L|x\ge s,\mathrm{\forall }s\in S\},S^l:=\{x\in L|x\le s,\mathrm{\forall }s\in S\}\end{array}$$

Notice that $S\subseteq T⟹S^u\supseteq T^u\wedge S^l\supseteq T^l.$$S\subseteq T\implies S^u\supseteq T^u\wedge S^l\supseteq T^l.$​

Proposition. $(-{)}^u⊣(-{)}^l$$(-)^u\dashv (-)^l$. i.e. $A^u\supseteq B⟺A^l\subseteq B$$A^u\supseteq B\iff A^l\subseteq B$. Whcih is obviously.

Appendix: Using Galois connection to prove Hilbert's Nullstellensatz

Definition.

Fix a natural number $n$$n$ and a field $K$$K$, consider the polynomial ring $K[X_1,...,X_n]$$K[X_1,...,X_n]$ and affine space $K^n$$K^n$​.

Let $S\subseteq K[X_1,...,X_n]$$S\subseteq K[X_1,...,X_n]$, define $V(S)=\{x\in K^n|f(x)=0\mathrm{\forall }f\in S\}$$V(S)=\{x\in K^n|f(x)=0\forall f\in S\}$.

Let $X\subseteq K^n$$X\subseteq K^n$, define $I(X)=\{f\in K[X_1,...,X_n]|f(x)=0\mathrm{\forall }x\in X\}$$I(X)=\{f\in K[X_1,...,X_n]|f(x)=0\forall x\in X\}$.

Proposition. Galois Connection between subsets of $K^n$$K^n$ and ideals of $K[X_1,...,X_n]$$K[X_1,...,X_n]$

$$\begin{array}{}\text{(14)}& I(X)\supseteq J⟺X\subseteq V(J)\end{array}$$

Proof.

Assume $I(X)\supseteq J$$I(X)\supseteq J$, then let $f\in J$$f\in J$, $\mathrm{\forall }x\in X,f(x)=0$$\forall x\in X,f(x)=0$. Hence $x\in X$$x\in X$ is a common zero of $J$$J$. Hence $X\subseteq V(J)$$X\subseteq V(J)$.

Suppose that $X\subseteq V(J)$$X\subseteq V(J)$, then $I(X)\supseteq IV(J)$$I(X)\supseteq IV(J)$. Since $IV(J)$$IV(J)$ is all the polynomial vanishing at $V(J)$$V(J)$, and $J$$J$ vanishing at $V(J)$$V(J)$, $I(X)\supseteq IV(J)\supseteq J,I(X)\supseteq J$$I(X)\supseteq IV(J)\supseteq J, I(X)\supseteq J$. $◻$$\square$

Recall that for a pair of Galois Connection $f,g,$$f,g,$ $\mathrm{Im}(f)\cong \mathrm{Im}(g)$$\mathrm{Im}(f)\cong\mathrm{Im}(g)$.

Since $fgf(a)=f(a)$$fgf(a)=f(a)$, $fg={\mathrm{Id}}_{\mathrm{Im}(f)}$$fg=\mathrm{Id}_{\mathrm{Im}(f)}$. Similarly, $gfg(b)=g(b)⟹gf={\mathrm{Id}}_{\mathrm{Im}(g)}$$gfg(b)=g(b)\implies gf=\mathrm{Id}_{\mathrm{Im}(g)}$​.

Observe that ${\mathrm{Im}}_I$$\mathrm{Im}_I$ is the set of radical ideal. Since if $f^n\in I(X)$$f^n\in I(X)$ then $f\in I(X)$$f\in I(X)$, and ${\mathrm{Im}}_V$$\mathrm{Im}_V$ is the set of variety.

Corollary. Hilbert's Nullstellensatz

There exists a order reversed isomorphism between the poset of variety and radical ideal.